In this article, you will learn a complete overview of section modulus such as its definition, types, formula with derivation for different sections, and much more.
Let’s know about each of the aspects related to section modulus in detail.
Section Modulus
Section Modulus is a geometric property used to calculate the bending stresses in a structural member.
Mathematically,
It is defined as the ratio of the moment of inertia of a section about its centroidal axis and to the distance of the extreme layer from the neutral axis.
It is denoted by Z.
Z = I/ymax
Mathematically By bending stress equation,
M/I = σmax/ymax
M = σmax × (I/ymax)
M = σmax × Z
Where,
I = Moment of Inertia(m⁴)
y = distance from NA to extreme layer(m)
The unit of section modulus is m³.
Types of Section Modulus
There are two types of section modulus:
- Elastic Section Modulus
- Plastic Section Modulus
Elastic Section Modulus
Elastic section modulus is calculated when we are to use the material behavior till the yield point.
For general design purposes, we use elastic section modulus.
Generally, elastic section modulus is denoted by Zₑ.
So,
Zₑ = I/ymax
Where,
I = Moment of inertia
ymax = Distance from NA to extreme layer
Elastic Section Modulus of Different Section
There are following different elastic section modulus:
Rectangular Section
As we know the moment of inertia of the rectangular section,
I = bd³/12
And the distance from the neutral axis,
ymax = d/2
So,
Zₑ = I/ymax
Zₑ = (bd³/12)/(d/2)
After calculating them,
Section modulus of rectangular section,
Zₑ = bd²/6
Hollow Rectangular Section
As we know the moment of inertia of the hollow rectangular section,
I = (BD³/12) - (bd³/12)
ymax = D/2
After putting these values,
Zₑ = I/ymax
(BD³/12) - (bd³/12)/(D/2)
Zₑ = (BD³ - bd³)/6D
Solid Circular
For solid Circular moment of inertia,
I = (π/64) × d⁴
ymax = d/2
Then,
Zₑ = {(π/64) × d⁴}/(d/2)
After calculating then find values of section modulus of solid circular
Zₑ = (π/32) × d³
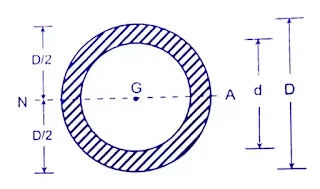
Hollow Circular
The moment of inertia of hollow Circular,
I = (π/64) × (D⁴ - d⁴)
And,
ymax = D/2
After putting these values,
Zₑ = (π/64) × (D⁴ - d⁴)/(D/2)
Zₑ = π/32 × {(D⁴ - d⁴)/D}
Symmetric I & C Section
Moment of inertia for the I & C section,
I = (BD³/12) - {(B - b)d³}/12
ymax = D/2
So,
Zₑ = [(BD³/12) - {(B - b)d³}/12]/(D/2)
Zₑ = {BD³ - (B - b)d³}/6D
Diamond
Elastic section modulus for diamond is,
Zₑ = bd²/24
Plastic Section Modulus
The plastic section modulus is used for materials where the elastic yield is acceptable and the plastic behavior is considered to be an acceptable range.
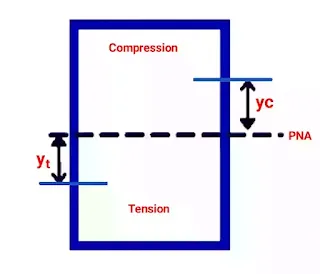
It depends on the location of the plastic neutral axis. The PNA is the axis that bisects the cross-section such that the compressive force from the region in compression is equal to the tension force from the region under tension. So, for sections with a constant yield stress, the area above and below the PNA will be equal, but for mixed sections, this is not necessarily the case.
Mathematically,
The plastic section modulus is the sum of the areas of cross-sections on each side of the plastic neutral axis that may or may not be equal and multiplied by the distance from the local centroid of the two regions to the plastic neutral axis.
Zₚ = (Ac × yc) + (Aₜ + yₜ)
Where,
Ac = Area of cross-section under compression.
Aₜ = Area of cross-section under tension.
yc = Distance from the plastic neutral axis to the center of gravity of the areas under compression.
yₜ = Distance from the plastic neutral axis to the center of gravity of areas under tension.
Since on the neutral axis, the area under compression is equal to the area under tension.
So,
Ac = Aₜ
And,
yc = yₜ
Plastic Section Modulus of Different Section
There are following section modulus for different section:
Rectangular Section
As we know,
on the neutral axis, the area under compression is equal to the area under tension.
So,
Ac = Aₜ
And,
yc = yₜ
Ac = Aₜ = bd/2
yc = yₜ = d/4
So,
Zₚ = (Ac × yc) + (Aₜ + yₜ)
Zₚ = (bd/2 × d/4) + (bd/2 × d/4))
After calculating
Zₚ = bd²/4
Similarly, we can calculate the section modulus of the rectangular hollow section,
Zₚ = (bd²/4) - (b- 2t) × {(b/2) - t}²
Circular Section
As we know, on the neutral axis, the area under compression is equal to the area under tension.
So,
Ac = Aₜ = πd²/8
yc = yₜ = 2d/3π
Zₚ = (πd²/8 × 2d/3π) + (πd²/8 × 2d/3π)
After calculating,
Zₚ = d³/6
Similarly, we can calculate the section modulus of the circular hollow section,
Circular hollow section,
Zₚ = (D³ - d³)/6
Related Article:
So here you have to know all aspects related to the section modulus. If you have any doubt then you are free to ask me by mail or on the contact us page.
Thank You.









0 Comments