In this article, you will learn a complete overview of maximum principal stress theory such as its definition, formula, calculation, and much more.
Maximum principal stress theory is the type of theory of failure which has already been discussed in the previous article.
When any materials come to static loads, which means that tensile, compressive, or bending stresses arise, the maximum principal stress theory is considered the basis of the design.
Maximum principal stress theory is used for only brittle material.
As per its name, Theory depends on principal stresses.
So before knowing the maximum principal stress theory first of all we have to know what is principal stress.
Principal Stress
Planes that have no shear stress are called principal planes.
Principal planes carry only normal stresses. These normal stresses are known as principal stress.
It may be maximum principal stress and minimum principal stress.
Maximum and minimum Principal stresses are represented by σ₁ and σ₂ respectively.
Maximum Principal Stress Theory
According to this theory, the failure of a machine component subjected to combined loading occurs whenever the maximum principal stress within the component becomes equal to the limiting strength ( yield for ductile and ultimate for brittle materials ) of the material in the Simple Tension Test.
This theory of failure is given by the British engineer, W.J.M. Rankine so this maximum principal stress theory is also called Rankine's Theory.
Consider a component with biaxial stresses subjected to it.
Then two principal stresses are produced on the body σ₁ and σ₂.
If the stress produced in the body due to the application of the load, is beyond limiting strength, permanent deformations occur in the body. Whenever permanent deformations in the body, occur the body is said to have failed.
This should be clear that failure does not mean rupture of the body.
So,
Failure occurs when Working stress is more than allowable stress,
Means σ₁ > σa
So for safety against failure,
σ₁ ≤ σa
Where,
σ₁ = maximum working stress
σa = allowable stress
For brittle material,
Factor of safety =
(Ultimate or yield tensile strength)/(Allowable working stress)
So,
FOS = (σy or σu)/σa
σa = (σy or σu)/FOS
Where,
σy = Yield stress
σu = Ultimate stress
So,
σ₁ ≤ σa
σ₁ ≤ (σy or σu)/FOS
Hence for safe design maximum working stress should be less than or equal to ultimate or yield stress and FOS must be greater than 1.
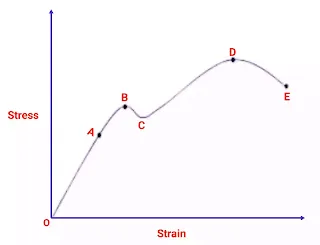
Now, Let us explain here the maximum principal stress theory by considering a component that is subjected to an external load and we have drawn the stress-strain curve here as shown in the following figure.
Point A
This is the proportionality limit; Up to this point, Hooke's law would be followed.
Point B
Point B is the elastic limit, up to this point the deformation would be elastic.
Point C
Point C is a low yield stress point.
Point D
It is the ultimate stress, this is the maximum value of stress in the stress-strain curve.
Point E
This point is the fracture point, up to this point the material will have only elastic and plastic deformation.
So we have to say that If the maximum value of the principal stress developed in the body is greater than point D means ultimate stress, then failure will occur.
Hence to avoid the failure condition of the component, the maximum value of the principal stress developed in the body should be less than the ultimate stress which means ultimate stress or yield stress.
Related Articles:
Calculation
Question
The principal stresses at a point in an elastic material are 100 N/mm ² ( tensile) and 80 N/mm² ( tensile ). If the ultimate stress in simple tension is 200 N /mm ², determine whether the failure of material will occur according to the maximum principal stress theory.
Solution
Given Data,
σ₁ = 100 N/mm²
σ₂ = 80 N/mm ²
σu = 200 N/mm ²
As we know that the failure of material will occur according to maximum principal stress theory when,
σ₁ > σa
100 N/mm ² > 200 N/mm ²
So clearly shows that σ₁ is less than the σa so failure will not occur.
So here you have to know all aspects related to the maximum principal stress theory if you have any doubt then you are free to ask me by mail or on the contact us page.
Thank You.







0 Comments